Cet article fait partie d’une série sur des projets ou papiers de recherche concernant l’apprentissage profond et le traitement automatique des langues. Bien que l’anglais soit très majoritairement maîtrisé dans notre domaine, apprendre dans sa langue maternelle reste plus agréable et efficace. Je fournirai pour chaque terme technique sa traduction en anglais (il arrivera parfois que je fasse le choix de conserver le terme anglais, lorsque celui ci est si souvent utilisé qu’il a été intégré au langage courant et où le terme français amène plus de confusion que celui en anglais) ainsi que les acronymes ou sigles associés !

Introduction

Je présente ici une explication des réseaux de Kolmogorov Arnold pour l’apprentissage profond, provenant du papier KAN: Kolmogorov–Arnold Networks, d’abord publié sur arXiv en 2024, puis publié à la conférence ICLR 2025 avec une nouvelle version corrigée (notamment en ajoutant de nouvelles expériences, en atténuant les affirmations fortes et en fournissant une analyse plus détaillée de la complexité).

Cet article va ainsi reprendre les parties principales du papier et va expliquer les différents concepts amenés par les auteurs.

Perceptron multi-couches

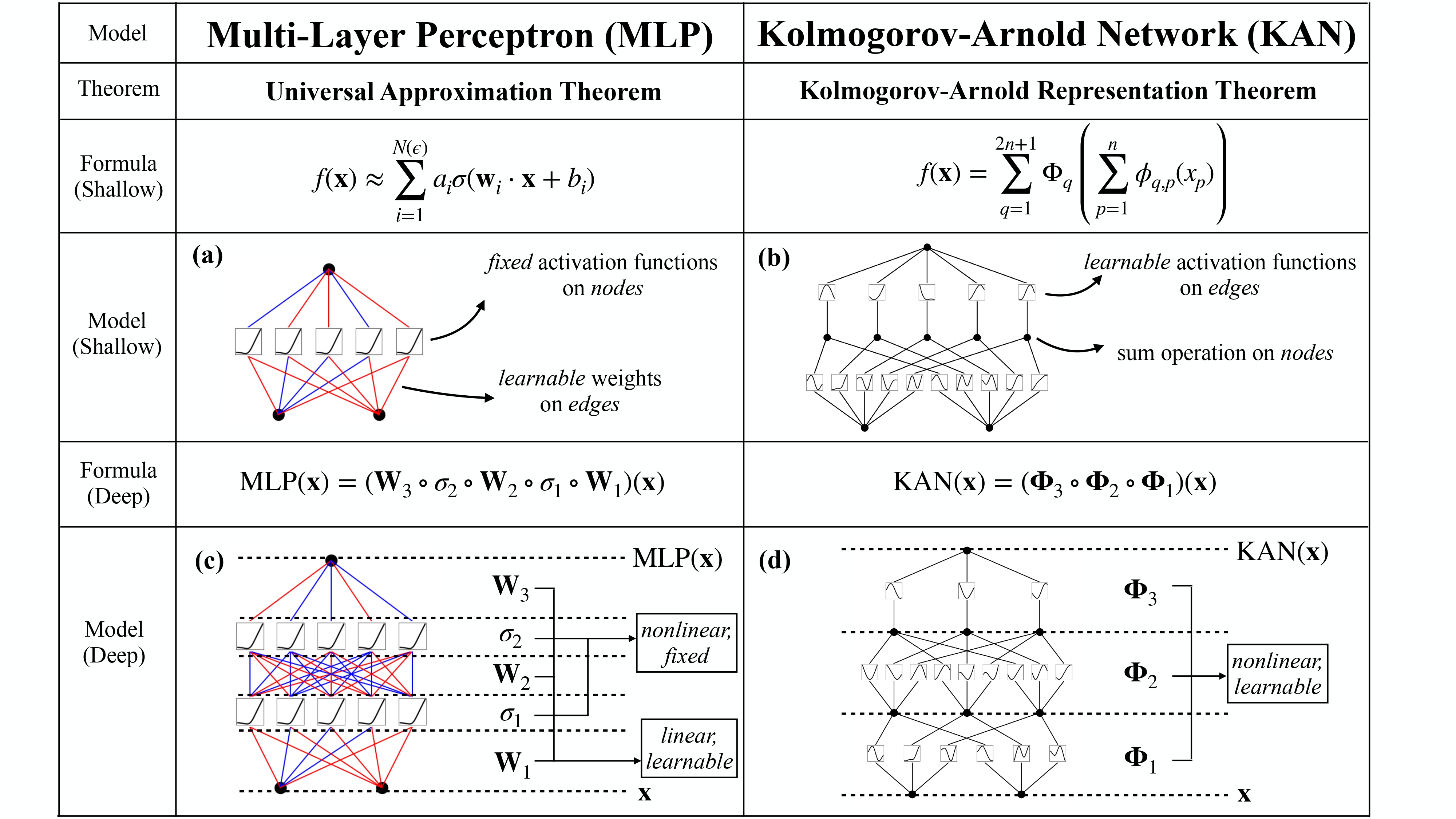
Je vais d’abord rappeler ce qu’est le perceptron multi-couches [multilayer perceptron / MLP], qu’on appelle aussi couches entièrement connectées à propagation avant [fully connected feedforward network]. Il s’agit d’un bloc essentiel des architectures de réseaux de neurones depuis très longtemps. La raison de cette durabilité ? Il s’agit de la méthode la plus efficace pour approximer des fonctions non linéaires. Il existe néanmoins des désavantages lorsqu’on utilise ce bloc. Les auteurs prennent l’exemple des Transformers : les MLP prennent la majorité des paramètres du modèle (hors embedding) et sont moins interprétables sans outil de post-analyse.

Ce bloc ce présente sous la forme de plusieurs Perceptrons ( = neurones) empilés sous forme de couche. On va ensuite créer plusieurs couches et les relier en associant la sortie de tous les neurones de la couche $n$ aux entrée des neurones de la couche $n+1$.

Théorème de Kolmogorov Arnold

Leur alternative est un nouveau bloc qu’ils appellent réseaux de Kolmogorov Arnold [Kolmogorov Arnold Networks ou KAN]. L’idée est qu’au lieu d’avoir des fonctions d’activations fixes sur les noeuds (neurones) comme dans les MLP (sigmoïdes, tangentes hyperboliques, ReLUs, etc.), on va ici avoir des fonctions d’activations apprenables sur les arètes (poids). Cette idée se base sur le théorème de représentation de Kolmogorov-Arnold qui dit que si $f$ est une fonction bornée continue à plusieurs variables alors $f$ peut être écrite comme une composition de fonctions continue à une seule variable et de l’opération binaire d’addition. Plus spécifiquement, pour une fonction de classe de régularité [smooth function] $f:[0,1]^n \longrightarrow \mathbb{R}$ :

\[f(x_1,...,x_n) = \sum\limits_{q=1}^{2n+1} \Phi_q \left(\sum\limits_{p=1}^{n} \phi_{q,p}(x_p)\right)\]

Où $\phi_{q,p} : [0,1] \longrightarrow \mathbb{R}$ et $\Phi_q : \mathbb{R} \longrightarrow \mathbb{R}$.

Il ne s’agit pas du premier article cherchant à utiliser ce théorème pour l’appliquer à l’apprentissage automatique. Cependant, ils cherchent ici à généraliser non pas uniquement à un réseau de profondeur 2 au maximum mais à n’importe quelle profondeur.

Schéma comparant les différentes propriétés des MLP et des KAN.

Focus sur un noeud particulier

Si l’on garde la comparaison avec le MLP, lorsqu’on se concentre sur un noeud, on obtient alors un perceptron, où s’il on a deux entrées $x_1,x_2 \in \mathbb{R}$ si l’on considère la fonction d’activation sigmoïde, et les poids entraînables $w_1,w_2 \in \mathbb{R}$ alors la sortie s’exprime ainsi : $output : \sigma(w_1x_1 + w_2x_2)$

Dans le cas de nos KAN , les arètes sont cette fois si des fonctions $f_1,f_2$ et où la “fonction d’activation” sera cette fois si simplement l’addition : $output : f_1(x_1) + f_2(x_2)$

Comment entraîner des fonctions ?

On souhaite ici entraîner nos fonctions avec une descente de gradient. Mais l’espace des fonctions est très varié et donc il peut y avoir de nombreux paramètres pour représenter des fonctions. La solution est de simplifier les fonctions.

Splines et B-Splines

Un bon moyen d’approximer des fonctions est en utilisant des Splines et plus précisément leur généralisation appelée B-splines.

Réseaux de Kolmogorov Arnold (KAN)