L'encodage positionnel | Mathieu Laï-king

Pourquoi a-t-on besoin de l’encodage positionnel ?

Dans un Transformer, chaque token est passé dans le réseau en parallèle (et non séquentiellement par exemple comme dans les réseaux de neurones récurrents). Ainsi, il faut ajouter dans la représentation un moyen de savoir la position de chaque token.

Requis

Il y a quelques propriétés que l’on voudrait que ces encodages possèdent :

Chaque position doit avoir le même identifiant (encodage positionnel) peu importe la taille de la séquence et peu importe les tokens composant la séquences. Ex : les position 1,2,3 de “Reine et roi” doivent être les mêmes que “Le roi est mort ce soir”
Vu que l’encodage positionnel “pousse” le vecteur original dans une certain direction, les valeurs de l’encodage (notamment de la 1ère dimension) ne doivent pas être trop larges, sinon elles pousseraient les vecteurs dans des sous-espaces bien distincts où la similarité/dissimilarité positionnelle cache la similarité sémantique

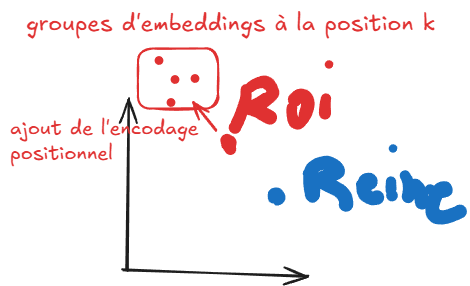
Schéma représentatif de l'encodage positionnel

Solution de “Attention is all you need”

Dans le papier “Attention is all you need” (Vaswani et al., 2017) une solution à ce problème est proposée. Ils déclarent :

“Dans ce travail, nous utilisons des fonctions sinus et cosinus de différentes fréquences :
$PE_{(pos,2i)} = \sin(pos/10000^{2i/d_{model}} )$ [positions paires]
$PE_{(pos,2i+1)} = \cos(pos/10000^{2i/d_{model}} )$ [positions impaires]
où
$d_{model}$ est le taille des embeddings (512),
$pos$ est la position [entier allant de 1 à la taille de la séquence]
$i$ est la dimension (allant de 0 à la taille de l’encodage).
En d’autres termes, chaque dimension du codage positionnel correspond à une sinusoïde. Les longueurs d’onde forment une progression géométrique de $2π$ à $10000 \cdot 2π$. Nous avons choisi cette fonction parce que nous avons émis l’hypothèse qu’elle permettrait au modèle d’apprendre facilement à suivre les positions relatives puisque pour n’importe quel seuil $k$ fixé, $PE_{pos+k}$ peut être représenté comme une fonction linéaire de $PE_{pos}$.
Nous avons également expérimenté l’utilisation de l’intégration positionnelle apprise (Gehring et al, 2017) à la place, et nous avons constaté que les deux versions produisaient des résultats presque identiques. Nous avons choisi la version sinusoïdale parce qu’elle peut permettre au modèle d’extrapoler à des séquences plus longues que celles rencontrées pendant l’apprentissage.”

Explication

La solution la plus simple à laquelle on pourrait penser est de prendre un encodage ou on ajout à chaque première position l’entier représentant sa position (donc une fonction f(n)=n): cepandant cela viole une des propriétés qui est que l’on ne veut pas des valeurs trop larges.

Ainsi les auteurs ont pensé à prendre des fonction bornée entre -1 et 1 : cosinus/sinus. Ces fonctions ont l’avantage d’être définies jusqu’a l’infini. Donc même si l’on a des taille de séquence très grandes, f(n) = cos(n) ou sin(n) sera toujours comprise entre -1 et 1.

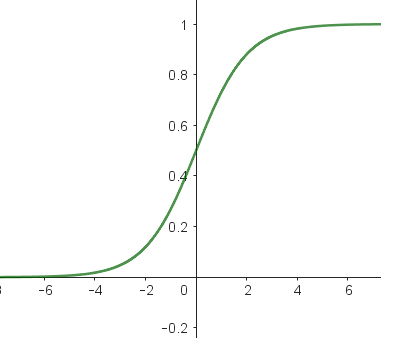
En comparaison à sigmoïde, qui est bornée entre 0 et 1, les sinus et cosinus ont l’avantage d’avoir une grande variabilité même pour des valeurs très grandes.

Sigmoïde

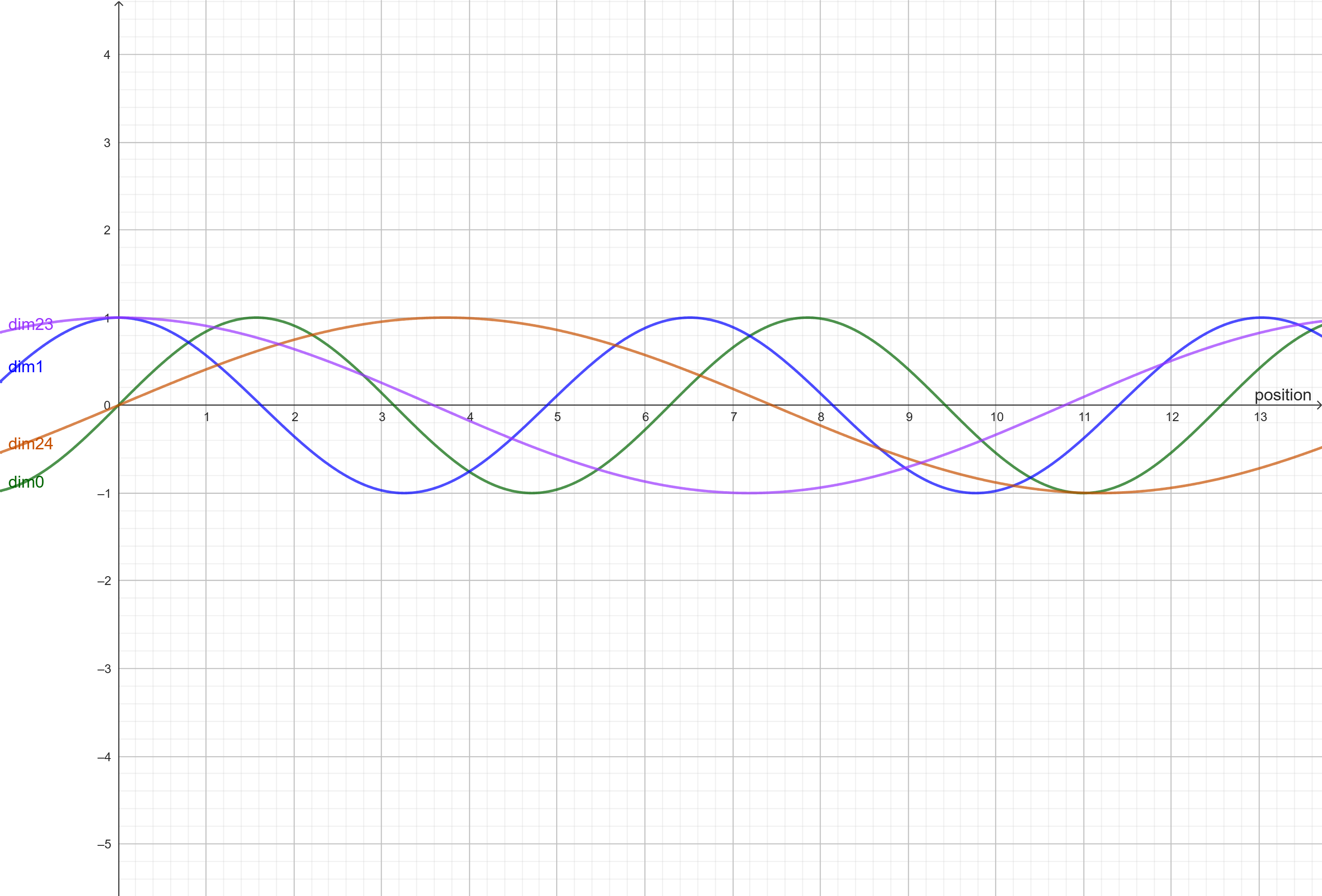
Après avoir choisi d’utiliser une fonction sinus, on remarque que le même résultat va se répéter pour différentes positions, ce qu’on ne souhaite pas. Une idée peut être de donner à notre fonction sinus une fréquence si faible que même pour notre plus grande taille de séquence, les nombre de ne répèteraient pas. mais ici on revient presque à la situation de départ avec la fonction linéaire (f(n)=n). on ne veut pas non plus que les valeurs des dimensions soient trop petites sinon la similarité sémantique va effacer la similarité de position.

La solution est donc d’utiliser justement le fait qu’on ait un vecteur large avec plusieurs dimensions et donc si une dimension est trop petite on va utiliser les autres pour bien montrer l’intention de démarquer la position dans le vecteur on va donc alter une dimension avec une fonction sinus et l’autre avec cosinus. et on va augmenter la fréquence du cosinus afin de différencier les valeurs alternées. et pour chaque token suivant, on va donc augmenter les fréquences du sinus et cosinus pour bien différencier leur position, et ainsi il y aura assez d’info pour que le transformer prenne en compte cette position.